Before implementing Fourier transform code, some foundation classes are needed.
The result calculated by the Fourier transform is a complex number (e.g., it has both a real and an imaginary part). So a container for a complex number is needed.
To apply Fourier transform algorithms we need some way to construct input data (e.g., a discretely sampled signal). In this case the input data is formed from a sequency of sine terms:
signal(x) = asin( Ax + o0 ) + bsin( Bx + o1 ) + csin( Cx + o2 ) ...
Where a, b, c... are coefficients that scale the result of the sin function, A, B, C... scale the argument to the sin function, oi is an offset factor that is added to the argument of sin.
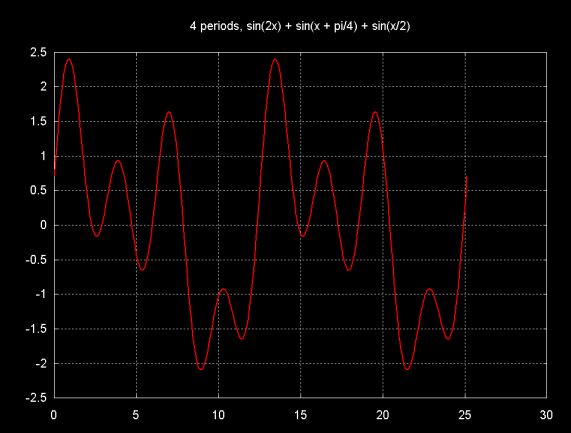
For example, the signal class can be used to generate
signal(x) = sin( 2x ) + sin( x + pi/4 ) + sin( 0.5x)
The graph is shown below

The Java source code for the foundation utility classes can be down loaded here
Ian Kaplan, September 2001
Revised:
Back to A Notebook Compiled While Reading Understanding Digital Signal Processing by Lyons