The coefficients that result from applying the Haar transform to a time series can be ordered by frequency. The Java code published with these web pages orders the coefficients in order of increasing frequency. For example, the AMAT close price time series consists of 512 points. The in-place Haar tranform replaces the data with a data point that represents the average over the time series (at index zero) and the coefficients for each spectrum. The number of coefficients in each spectrum is a power of two (e.g., 1, 2, 4, 8, 16, 32, 64, 128, 256).
A given spectrum can be removed from the time series by setting the coefficients to zero and then applying the inverse wavelet transform. The graphs below show the AMAT close price time series with various spectrum removed. In all cases the spectrum 1, 2, 4, 8, 16, 32 are included. The result of the inverse Haar transform is graphed in blue. The AMAT close price time series is shown in red.

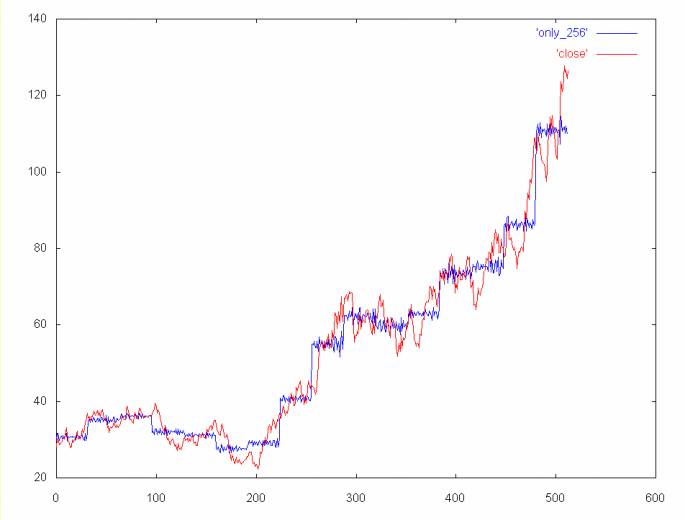
Coefficient spectrum 1, 2, 4, 8, 16, 32 and 256
This reconstruction of the time series shows the high frequency noise spectrum (elements 256 to 511) on top of the time series "back bone".
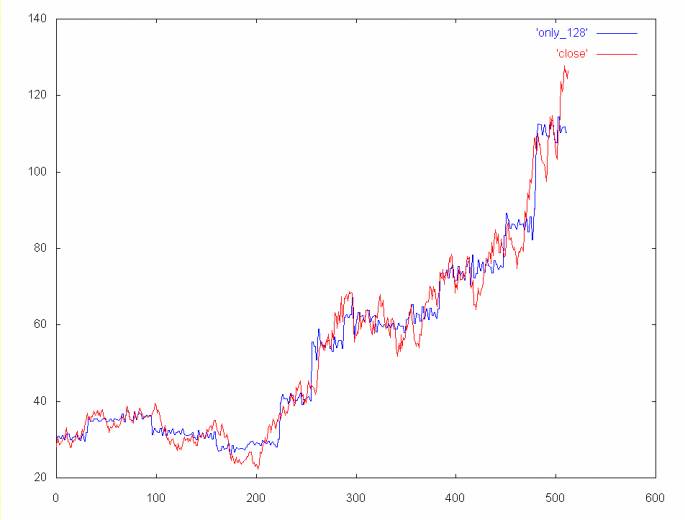
Coefficient spectrum 1, 2, 4, 8, 16, 32 and 128
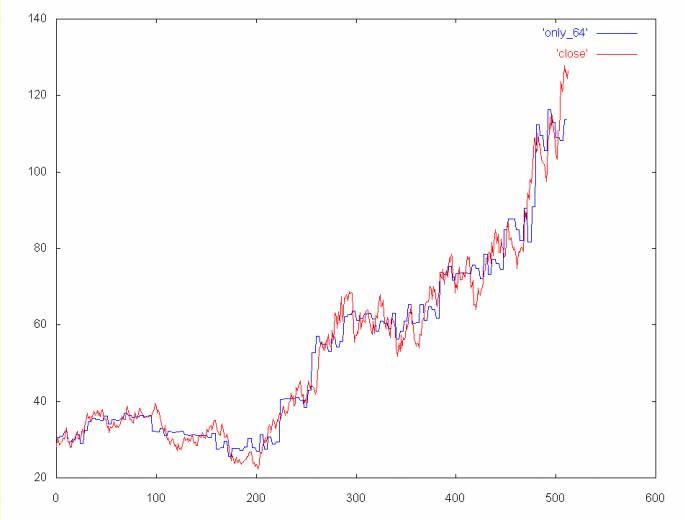
Coefficient spectrum 1, 2, 4, 8, 16, 32 and 64
The graphs below show the time series with one or more spectrum removed. The first graph shows the time series without the high frequency spectrum. The next two graphs show the time series without the high frequency spectrum and one of the lower frequency spectrums. The high frequency spectrum is removed because it tends to obscure the details of the contribution of the lower frequency spectrum.
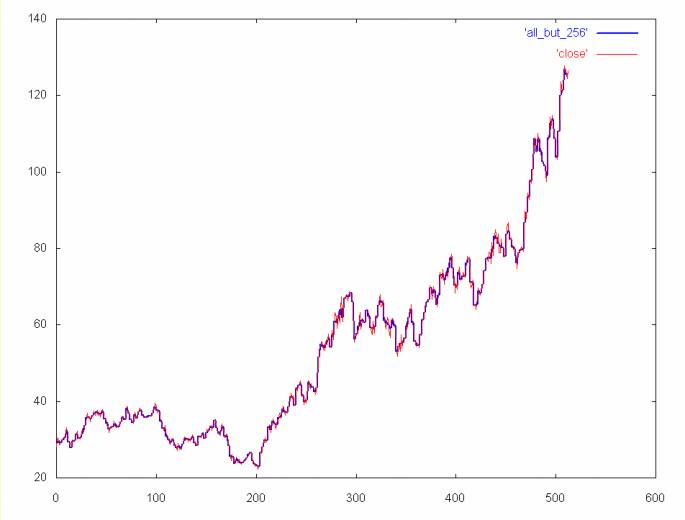
Time series without the 256 spectrum (e.g., coefficient spectrum 1, 2, 4, 8, 16, 32, 64, 128)
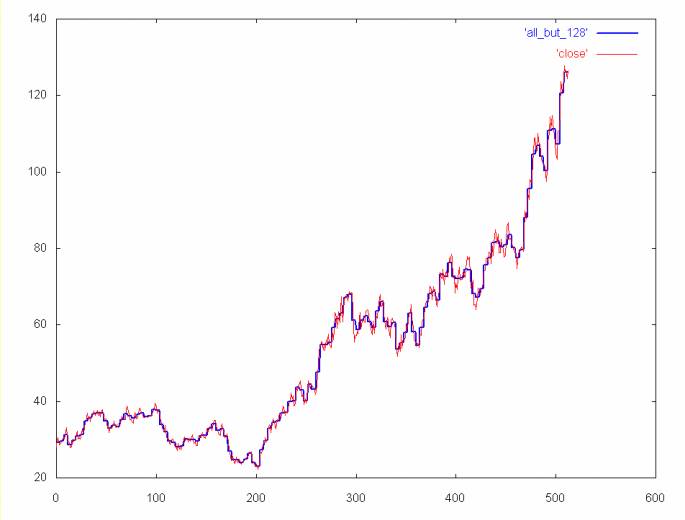
Time series without the 128 and 256 spectrum (e.g., coefficient spectrum 1, 2, 4, 8, 16, 32, 64)
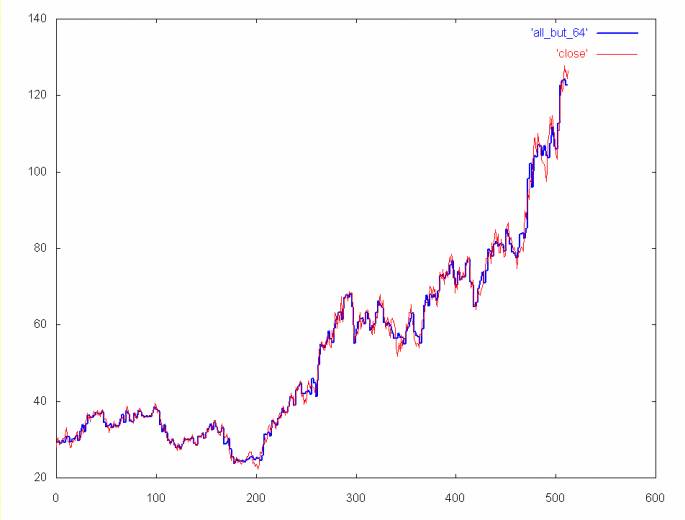
Time series without the 64 and 256 spectrum (e.g., coefficient spectrum 1, 2, 4, 8, 16, 32, 128)
Ian Kaplan, July 2001
Revised:
back to Applying the Haar Wavelet Transform to Time Series Information