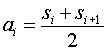
This web page was written to provide some background explaining the structure of wavelet algorithms covered on companion web pages. The structure of wavelet transforms like the Daubechies D4 transform can be more clearly explained in the context of linear algebra (e.g., matrices).
Wavelet algorithms like the Daubechies D4 transform have special cases that must be handled in real applications with finite data sets. There are several methods for addressing the edge problem. One of these is Gram-Schmidt orthogonalization, which is a matrix technique from linear algebra.
Linear algebra provides a tool for illuminating some wavelet algorithms and for developing wavelet and scaling function coefficients for the edges of a finite signal. In practice matrices are not used to calculate the wavelet transform. The matrix form of the wavelet transform is both computationally inefficient and impractical in its memory consumption. A single wavelet transform step using a matrix algorithm involves the multiplication of the signal vector by a transform matrix, which is an ON2 operation (where N is the data size for each transform step). In contrast, each step of the standard transform has a computational complexity of ON.
Each step in the forward Haar transform calculates a set of wavelet coefficients and a set of averages. If a data set s0, s1, ... sN-1 contains N elements, there will be N/2 averages and N/2 coefficient values. The averages are stored in the lower half of the N element array and the coefficients are stored in the upper half. The averages become the input for the next step in the wavelet calculation, where for iteration i+1, Ni+1 = Ni/2. The recursive iterations continue until a single average and a single coefficient are calculated. This replaces the original data set of N elements with an average, followed by a set of coefficients whose size is an increasing power of two (e.g., 20, 21, 22 ... N/2 ).
The Haar equations to calculate an average (ai) and a wavelet coefficient (ci) from an odd and even element in the data set are shown below:
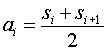
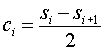
In wavelet terminology the Haar average is calculated by the scaling function. The coefficient is calculated by the wavelet function.
The data input to the forward transform can be perfectly reconstructed using the following equations:

In the linear algebra view of the forward Haar transform, the first average is calculated by the inner product of the signal [s0, s1, ... sN-1] and the vector, of the same size, [0.5, 0.5, 0, 0, ..., 0]. This is the scaling vector. The first coefficient is calculated by the inner product of the signal and the vector [0.5, -0.5, 0, 0, ..., 0]. This is the wavelet vector.
The next average and coefficient are calculated by shifting the scaling and wavelet vectors by two and calculating the inner products.
In the wavelet literature scaling and wavelet values are sometimes represented by hi and gi respectively. In the case of the Haar transform the scaling and wavelet values would be
scaling function coefficients h0 = 0.5 h1 = 0.5 wavelet function coefficients g0 = 0.5 g1 = -0.5
The scaling and wavelet values for the Haar transform are shown below in matrix form.

The first step of the forward Haar transform for an eight element signal is shown below. Here signal is multiplied by the forward transform matrix.

The arrow represents a split operation that reorders the result so that the average values are in the first half of the vector and the coefficients are in the second half. To complete the forward Haar transform there are two more steps. The next step would multiple the ai values by a 4x4 transform matrix, generating two new averages and two new coefficients which would replace the averages in the first step. The last step would multiply these new averages by a 2x2 matrix generating the final avarage and the final coefficient.
Like the forward Haar transform, a step in the inverse Haar transform can be described in linear algebra terms. The matrix operation to reverse the first step of the Haar tranform for an eight element signal is shown below.

In this case the arrow represents a merge operation that interleaves the averages and the coefficients.
Java software that implements the forward and inverse Haar transform using matrices can be downloaded here. This software includes a modest linear algebra class (e.g., matrix multiply and various vector operations).
One of the struggles I've had with the wavelet literature is the terminology. As with any field of specialty, mathematics assumes a shared basic set of knowledge, which includes areas like linear algebra. The wavelet literature in some cases seems to be written for those with a graduate level background in mathematics. This certainly does not describe my background. I am not a mathematician and the linear algebra I know is self taught.
The wavelet literature sometimes refers to wavelet basis functions. Given my shallow background in linear algebra, I feel a bit unsure defining these terms, but I'll walk out on a limb (if I'm wrong, please send me e-mail with the correct explanation, preferably couched in the kind of simple terms used here).
The 8x8 matrix above has a row and column basis of 8 (which is
sometimes represented as  ).
A wavelet basis function refers to the number of coefficients in
the scaling and wavelet function. The Haar transform has an
R2 basis and the Daubechies D4 has an
R4 basis.
).
A wavelet basis function refers to the number of coefficients in
the scaling and wavelet function. The Haar transform has an
R2 basis and the Daubechies D4 has an
R4 basis.
Wavelet packets attempt to find the "best basis". The details of wavelet packets are beyond this web page, but in this case "basis" refers to the region of the original signal over which the scaling or wavelet function is applied.
Looked at in terms of the matrix operations discussed on this web page, the scaling and wavelet functions apply to matrix rows (row basis). With each step of the wavelet calculation the basis changes (e.g., in this example, from 8, to 4, to 2). Conceptually the scaling and wavelet functions span larger and larger sections of the signal as the basis decreases. In the case of the Haar transform, as the basis gets smaller the averages and differences represent the average or average change over larger and larger portions of the signal.
As noted above, the Haar scaling and wavelet functions are calculated using two coefficients, h0, h1 and g0, g1, respectively. As the name suggests, the scaling and wavelet functions of the Daubechies D4 wavelet transform are calculated using four coefficients, h0, h1, h2, h3 and g0, g1, g2, g3. The derivation for the coefficient values can be found in Ingrid Daubechies work and in section 5.5 of Wavelets and Filter Banks by Gilbert Strang and Truong Nguyen, Wellesley-Cambridge Press, 1997.
The scaling function coefficient values are:
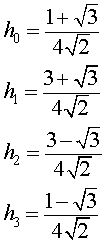
The wavelet function coefficient values are:
g0 = h3
g1 = -h2
g2 = h1
g3 = -h0
The scaling values, ai, and the wavelet values, ci are calculated by taking the inner product of the hj and gj coefficients and the signal. The equations for the scaling and wavelet inner products are shown below. The second verson of each equation shows the indexing of the signal.
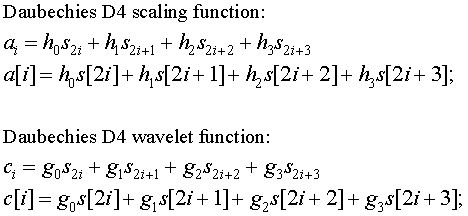
As with the Haar transform discussed above, the Daubechies scaling and wavelet function coefficients shift from right to left by two places in each iteration of a wavelet transform step.
The Daubechies transform has no special cases when applied to an infinite signal. In the finite world outside of mathematics there would be a signal with N elements (ranging from s[0] to s[N-1]). When the scaling and wavelet functions are shifted so that the value of i in the equations above is N-3, two coefficients will stick out beyond the end of the signal (e.g., the inner product will be calculated with s[N] and s[N+1]). Methods for dealing with this are discussed on my Daubechies wavelet web page.
Although in practice we don't have infinite signals (or transform matrices) ignoring the special cases allows us to look at the Daubechies transform as a matrix, showing the structure of the coefficients.
Daubechies forward transform matrix

The inverse Daubechies D4 transform matrix is the transpose of the forward transform matrix:
Daubechies inverse transform matrix

The wavelet literature covers a wide variety of wavelet algorithms, which are drawn from an infinite set of wavelet algorithms. When I first started reading about wavelets one of the first questions I had was "which algorithm should I use". The choice of the wavelet algorithm depends on the application.
The result of the wavelet transform produces a "down sampled" smoothed version of the signal (calculated by the wavelet scaling function) and a "down sampled" version of the signal that reflects change between signal elements. The smoothing function is sometimes referred to as a low pass filter. The wavelet function is sometimes referred to as a high pass filter.
If we compare the Haar forward transform matrix to the Daubecies D4 transform matrix, we can see that there is no overlap between successive pairs of scaling and wavelet functions, as there is with the Daubechies transform.
The Haar high pass filter (wavelet function) produces a result that reflects the difference between an even element and an odd element. The difference between an odd element and its even successor will not be reflected in the coefficient band calculated by a single step of Haar high pass filter (although this change will be picked up by later steps). In contrast, there is overlap between successive Daubechies high pass filters, so change between any two elements will be reflected in the result.
The Daubechies D4 wavelet transform is more "accurate", since change in the input data set is reflected in the high pass filter results at each transform step. The cost if using the Daubechies algorithm is higher computation overhead (twice the number of operations, compared to Haar) and a more complicated algorithm (the algorithm must properly handle the edge condition where i=0). Whether the higher accuracy of the Daubechies algorithm is worth the cost is application dependent.
Wavelets and Filter Banks by Gilbert Strang and Truong Nguyen, Wellesley-Cambridge Press, 1997
Strang and Nguyen make heavy use of linear algebra in their coverage of wavelets and wavelet filters. As noted above, this text also include the derivation of the Daubechies wavelet functions. This book is most easily read by a reader with a background in digital signal processing and linear algebra.
Ripples in Mathematics: the Discrete Wavelet Transform by Arne Jense and Anders la Cour-Harbo, Springer, 2001
So far this is the best book I've been able to find on wavelets, from an implementation point of view. Ripples provides less mathematical depth than Strange and Nguyen, but the material is more accessible.
Ian Kaplan, January 2002
Revised: