This web page publishes a C++ program that generates a cascade multiplier. The design for this multiplier comes from Joseph J.F. Cavanagh's excellent book on computer arithmetic, Digital Computer Arithmetic: Design and Implementation, 1984. Sadly this book is out of print. My copy of this book was printed before books were commonly printed on acid free paper and the pages are starting to yellow. Although this book is almost twenty years old, computer arithmetic remains the same. The only thing that has changed is the density of VLSI chips. Hardware modules like the cascade multiplier, discussed here, consumed too much hardware area in some cases. Given current chip density, a 32x32 multiplier can be included in a microprocessor.
I implemented this multiplier because I wanted a large structural Verilog test case for Quickturn's SimServer hardware accelerated behavioral simulation system. I was also fascinated by the tiling and recursive nature of the multiplier. The multiplier implemented here is not the most efficient in its use of hardware nor the fastest in terms of logic levels. Cavanagh shows how 4X4 adder slices can be combined with a look ahead carry tree (a so called Wallace tree) to build larger multipliers, which are faster than this multiplier for larger bit widths.
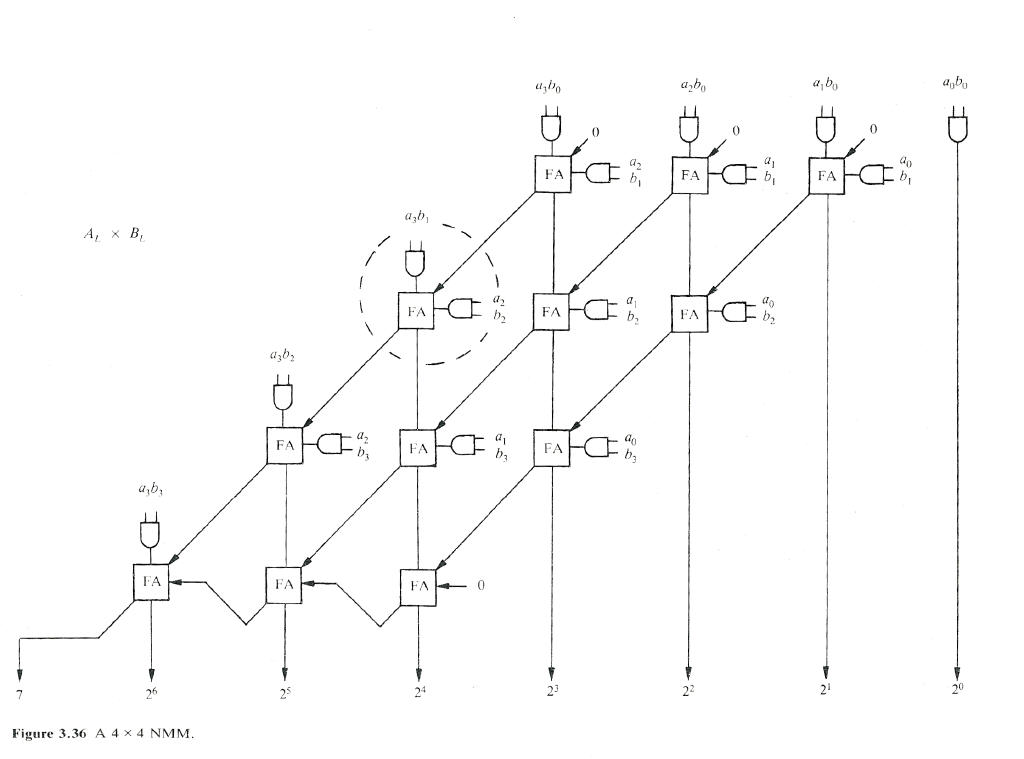
The figure below shows what I have been referring to as a cascade multiplier. The multiplier shown here takes two 4-bit operands (e.g., its a 4 X 4 multiplier) and generates an 8-bit result. The FA elements in the diagram are full adders. This version of the multiplier does unsigned multiplication. A slight variation on this design will perform signed integer multiplication.

Figure 3.36, A 4 X 4 NMM (nonadditive multiply module), pg 192, Digital Computer Arithmetic by Joseph J.F. Cavanagh, 1984
I'm not sure why Cavanagh refers to this as a nonadditive multiply module, since it is clearly using addition. The cascade multiplier generation program generates structural Verilog plus a small behavioral Verilog testbench. This test bench is only useful for testing small multiplier, since it tests all combinations of operands. The automaticly generated Verilog multiplier is shown below. It has been edited slightly for HTML formatting and readability (e.g., the module names are shown in bold, etc..)
module full_addr( a, b, c_in, c_out, sum );
input a, b, c_in;
output sum, c_out;
wire a1, a2, a3, a4;
wire c1, c2, c3, c4;
assign a1 = (~a) & (~b) & c_in;
assign a2 = (~a) & b & (~c_in);
assign a3 = a & (~b) & (~c_in);
assign a4 = a & b & c_in;
assign sum = a1 | a2 | a3 | a4;
assign c1 = (~a) & b & c_in;
assign c2 = a & (~b) & c_in;
assign c3 = a & b & (~c_in);
assign c4 = a & b & c_in;
assign c_out = c1 | c2 | c3 | c4;
endmodule
module mult( A, B, rslt );
input [ 3:0] A, B;
output [ 7:0] rslt;
wire a00, a01, a02, a03;
wire b00, b01, b02, b03;
wire r00, r01, r02, r03, r04, r05, r06, r07;
wire c00, c01, c02, c03, c04, c05, c06, c07;
wire c08, c09, c10, c11;
assign a00 = A[ 0];
assign a01 = A[ 1];
assign a02 = A[ 2];
assign a03 = A[ 3];
assign b00 = B[ 0];
assign b01 = B[ 1];
assign b02 = B[ 2];
assign b03 = B[ 3];
assign rslt[ 0] = r00;
assign rslt[ 1] = r01;
assign rslt[ 2] = r02;
assign rslt[ 3] = r03;
assign rslt[ 4] = r04;
assign rslt[ 5] = r05;
assign rslt[ 6] = r06;
assign rslt[ 7] = r07;
assign r00 = a00 & b00;
full_addr fa000 (a01 & b00, a00 & b01, 1'b0, c00, s00);
full_addr fa001 (a02 & b00, a01 & b01, 1'b0, c01, s01);
full_addr fa002 (a03 & b00, a02 & b01, 1'b0, c02, s02);
assign r01 = s00;
full_addr fa003 (s01 , a00 & b02, c00, c03, s03);
assign r02 = s03;
full_addr fa004 (s02 , a01 & b02, c01, c04, s04);
full_addr fa005 (a03 & b01, a02 & b02, c02, c05, s05);
full_addr fa006 (s04 , a00 & b03, c03, c06, s06);
assign r03 = s06;
full_addr fa007 (s05 , a01 & b03, c04, c07, s07);
full_addr fa008 (a03 & b02, a02 & b03, c05, c08, s08);
full_addr fa009 (s07 , 1'b0, c06, c09, s09);
assign r04 = s09;
full_addr fa010 (s08 , c09, c07, c10, s10);
assign r05 = s10;
full_addr fa011 (a03 & b03, c10, c08, c11, s11);
assign r06 = s11;
assign r07 = c11;
endmodule
module testbench;
reg [ 3:0] A, B;
wire [ 7:0] rslt;
mult mult_inst (A, B, rslt);
initial
begin : init
parameter FALSE = 0;
parameter TRUE = 1;
reg [ 4:0] i, j;
reg passed;
passed = TRUE;
for (j = 1; j < 16; j = j + 1)
begin
for (i = 1; i < 16; i = i + 1)
begin
A = i;
B = j;
#1;
if (rslt != i * j)
begin
passed = FALSE;
$display("test failed for %d x %d", i, j );
end // if
end // for i
end // for j
if (passed)
$display("test passed");
else
$display("test failed");
$finish;
end
endmodule
The C++ code that generates the cascade multiplier is shown below. Elsewhere on the bearcave.com web pages I've been critical of the fact that most programmers do not document their software. For most large projects I try to make sure that my software is clearly documented. But like a lot of programmers, I'm embarrassed to say that I'm guilty of not providing much documentation for small hacks like this one. Even small hacks can be useful later, so this is clearly not good practice.
The source code below has been formatted for HTML. You an download the original, unformatted code here
/*
Generate Verilog for a combinatoric multiplier
This program generates the Verilog for a combinatoric multiplier
that is built out of cascaded full adders. The program is given a
command line argument for the width of the multiplier operands. It
generates the full adder module, the multiplier and the associated
test bench, which tests the multiplier through the complete range.
This means that for values larger than 8 the verilog generated
takes a long time to simulate on Verilog XL.
The multipler in created by this program is based on the cascade
multiplier described in "Digital Computer Arithmetic" by Joseph
J.F. Cavanagh, McGraw-Hill, 1984
To compile on Solaris
CC genmult.C -o genmult
To run
genmult
For example
genmult 4
Author:
Ian Kaplan
Copyright and use:
You are granted the use of this software without limitation as
long as you include
Copyright Ian Kaplan, iank@bearcave.com
*/
#include <ctype.h>
#include <string.h>
#include <stdio.h>
enum {
#ifndef FALSE
FALSE = 0,
#endif
#ifndef TRUE
TRUE = 1,
#endif
bogus_filler };
int get_size( char *num_str )
{
int strok, len, i;
int size;
size = 0;
len = strlen( num_str );
strok = TRUE;
// check to make sure that all the characters in
// the string are digits.
for (i = 0; i < len; i++) {
if (! isdigit( num_str[i] )) {
strok = FALSE;
break;
}
}
// if the string is OK, convert it to an integer
if (strok) {
sscanf( num_str, "%d", &size );
}
return size;
} // get_size
void
gen_adder(FILE *fp)
{
fprintf(fp, "\n");
fprintf(fp, "module full_addr( a, b, c_in, c_out, sum );\n");
fprintf(fp, "input a, b, c_in;\n");
fprintf(fp, "output sum, c_out;\n");
fprintf(fp, "\n");
fprintf(fp, "wire a1, a2, a3, a4;\n");
fprintf(fp, "wire c1, c2, c3, c4;\n");
fprintf(fp, "\n");
fprintf(fp, " assign a1 = (~a) & (~b) & c_in;\n");
fprintf(fp, " assign a2 = (~a) & b & (~c_in);\n");
fprintf(fp, " assign a3 = a & (~b) & (~c_in);\n");
fprintf(fp, " assign a4 = a & b & c_in;\n");
fprintf(fp, " assign sum = a1 | a2 | a3 | a4;\n");
fprintf(fp, "\n");
fprintf(fp, " assign c1 = (~a) & b & c_in;\n");
fprintf(fp, " assign c2 = a & (~b) & c_in;\n");
fprintf(fp, " assign c3 = a & b & (~c_in);\n");
fprintf(fp, " assign c4 = a & b & c_in;\n");
fprintf(fp, " assign c_out = c1 | c2 | c3 | c4;\n");
fprintf(fp, "\n");
fprintf(fp, "endmodule\n");
fprintf(fp, "\n");
} // get_adder
void
gen_header( unsigned int mult_size, FILE *fp = stdout )
{
fprintf(fp, "module mult( A, B, rslt );\n");
fprintf(fp, "input [%2d:0] A, B;\n", mult_size-1 );
fprintf(fp, "output [%3d:0] rslt;\n\n", (mult_size * 2)-1 );
} // gen_header
void gen_end( FILE *fp )
{
fprintf(fp, "endmodule\n");
} // gen_end
void
gen_mult( unsigned int mult_size, FILE *fp = stdout )
{
int i, j, addr_cnt, rslt_cnt;
fprintf(fp, " assign r00 = a00 & b00;\n");
addr_cnt = 0;
for (i = 0; i < mult_size - 1; i++) {
fprintf(fp, " full_addr fa%03d (", addr_cnt );
fprintf(fp, "a%02d & b00, a%02d & b01, 1'b0, c%02d, s%02d",
i + 1, i, addr_cnt, addr_cnt );
fprintf(fp, ");\n");
addr_cnt++;
}
fprintf( fp, " assign r01 = s00;\n\n");
rslt_cnt = 2;
for ( j = 2; j < mult_size; j++ ) {
for (i = 0; i < mult_size - 1; i++) {
if (i < mult_size - 2) {
fprintf(fp, " full_addr fa%03d (", addr_cnt );
// module full_adder( a, b, c_in, sum, c_out );
fprintf(fp, "s%02d , a%02d & b%02d, c%02d, c%02d, s%02d",
addr_cnt - (mult_size-2), i, j, addr_cnt - (mult_size-1),
addr_cnt, addr_cnt );
fprintf(fp, ");\n");
if (i == 0) {
fprintf( fp, " assign r%02d = s%02d;\n", rslt_cnt, addr_cnt );
}
}
else {
fprintf(fp, " full_addr fa%03d (", addr_cnt );
fprintf(fp, "a%02d & b%02d, a%02d & b%02d, c%02d, c%02d, s%02d",
i+1, j - 1, i, j, addr_cnt - (i+1), addr_cnt, addr_cnt );
fprintf(fp, ");\n");
}
addr_cnt++;
}
rslt_cnt++;
fprintf(fp, "\n");
}
for (i = 0; i < mult_size - 2; i++) {
if (i == 0) {
fprintf(fp, " full_addr fa%03d (", addr_cnt );
// module full_adder( a, b, c_in, sum, c_out );
fprintf(fp, "s%02d , 1'b0, c%02d, c%02d, s%02d",
addr_cnt - (mult_size-2), addr_cnt - (mult_size-1),
addr_cnt, addr_cnt );
fprintf(fp, ");\n");
}
else {
fprintf(fp, " full_addr fa%03d (", addr_cnt );
// module full_adder( a, b, c_in, sum, c_out );
fprintf(fp, "s%02d , c%02d, c%02d, c%02d, s%02d",
addr_cnt - (mult_size-2), addr_cnt -1, addr_cnt - (mult_size-1),
addr_cnt, addr_cnt );
fprintf(fp, ");\n");
}
fprintf( fp, " assign r%02d = s%02d;\n", rslt_cnt, addr_cnt );
addr_cnt++;
rslt_cnt++;
}
fprintf(fp, " full_addr fa%03d (", addr_cnt );
fprintf(fp, "a%02d & b%02d, c%02d, c%02d, c%02d, s%02d",
mult_size-1, mult_size-1, addr_cnt-1, addr_cnt - (mult_size-1),
addr_cnt, addr_cnt );
fprintf(fp, ");\n");
fprintf(fp, "\n");
fprintf( fp, " assign r%02d = s%02d;\n",
mult_size + (mult_size -2), addr_cnt );
fprintf( fp, " assign r%02d = c%02d;\n",
mult_size + (mult_size - 1), addr_cnt );
} // gen_mult
void
gen_vars(int mult_size, char *name, FILE *fp )
{
int i, semi;
for (i = 0; i < mult_size; i++) {
semi = FALSE;
if ((i % 8) == 0) {
if (i > 0) {
fprintf(fp, ";\n");
semi = TRUE;
}
fprintf( fp, "wire ");
}
else if (i < mult_size )
fprintf(fp, ", ");
fprintf( fp, "%s%02d", name, i );
}
if (! semi)
fprintf(fp, ";\n");
}
void
gen_assign( unsigned int mult_size, char *dest, char *src, FILE *fp )
{
int i;
for (i = 0; i < mult_size; i++) {
fprintf(fp, " assign %s%02d = %s[%2d];\n", dest, i, src, i );
}
} // gen_assign
void
gen_assign2( unsigned int mult_size, char *dest, char *src, FILE *fp )
{
int i;
for (i = 0; i < mult_size; i++) {
fprintf(fp, " assign %s[%2d] = %s%02d;\n", dest, i, src, i );
}
} // gen_assign
void
gen_assigns( unsigned int mult_size, FILE *fp )
{
gen_vars(mult_size, "a", fp);
fprintf(fp, "\n");
gen_vars(mult_size, "b", fp);
fprintf(fp, "\n");
gen_vars(mult_size * 2, "r", fp );
fprintf(fp, "\n");
gen_vars(mult_size * (mult_size-1), "c", fp);
fprintf(fp, "\n");
gen_assign(mult_size, "a", "A", fp );
fprintf(fp, "\n");
gen_assign(mult_size, "b", "B", fp );
fprintf(fp, "\n");
gen_assign2(mult_size * 2, "rslt", "r", fp );
fprintf(fp, "\n");
} // gen_assigns
void
gen_mult_module( unsigned int mult_size, FILE *fp )
{
gen_header( mult_size, fp );
gen_assigns( mult_size, fp );
gen_mult( mult_size, fp );
gen_end( fp );
} // gen_mult_module
void
gen_testbench( unsigned int mult_size, FILE *fp )
{
fprintf(fp, "\n");
fprintf(fp, "module testbench;\n");
fprintf(fp, "reg [%2d:0] A, B;\n", mult_size-1);
fprintf(fp, "wire [%2d:0] rslt;\n", (mult_size * 2)-1);
fprintf(fp, "\n");
fprintf(fp, " mult mult_inst (A, B, rslt);\n");
fprintf(fp, "\n");
fprintf(fp, " initial\n");
fprintf(fp, " begin : init\n");
fprintf(fp, " parameter FALSE = 0;\n");
fprintf(fp, " parameter TRUE = 1;\n");
fprintf(fp, " reg [%2d:0] i, j;\n", mult_size);
fprintf(fp, " reg passed;\n");
fprintf(fp, "\n");
fprintf(fp, " passed = TRUE;\n");
fprintf(fp, " for (j = 1; j < %2d; j = j + 1)\n", 1 << mult_size);
fprintf(fp, " begin\n");
fprintf(fp, " for (i = 1; i < %2d; i = i + 1)\n", 1 << mult_size );
fprintf(fp, " begin\n");
fprintf(fp, " A = i;\n");
fprintf(fp, " B = j;\n");
fprintf(fp, " #1;\n");
fprintf(fp, " if (rslt != i * j)\n");
fprintf(fp, " begin\n");
fprintf(fp, " passed = FALSE;\n");
fprintf(fp, " $display(\"test failed for %%d x %%d\", i, j );\n");
fprintf(fp, " end // if\n");
fprintf(fp, " end // for i\n");
fprintf(fp, " end // for j\n");
fprintf(fp, "\n");
fprintf(fp, " if (passed)\n");
fprintf(fp, " $display(\"test passed\");\n");
fprintf(fp, " else\n");
fprintf(fp, " $display(\"test failed\");\n");
fprintf(fp, " $finish;\n");
fprintf(fp, " end\n");
fprintf(fp, "\n");
fprintf(fp, "endmodule\n");
fprintf(fp, "\n");
} // gen_testbench
void
gen_verilog( unsigned int mult_size, FILE *fp = stdout )
{
gen_adder( fp );
gen_mult_module( mult_size, fp );
gen_testbench( mult_size, fp );
} // gen_verilog
int
main(int argc, char *argv[] )
{
int status;
char *progname;
progname = argv[ 0 ];
status = 0;
if (argc != 2) {
printf("usage: %s <multiplier size>\n", progname );
status = 1;
}
else {
unsigned mult_size;
mult_size = get_size( argv[ 1 ] );
if (mult_size > 0) {
gen_verilog( mult_size );
}
else {
printf("usage: size should be greater than zero\n", progname );
status = 1;
}
}
return status;
}
Ian Kaplan
July 2001
back to VLSI Design and Simulation