The (Mis)behavior of Markets: A Fractal View of Risk, Ruin, and Reward
Benoit Mandelbrot and Richard L. Hudson
Basic Books, 2004
Review score: *** out of *****
Benoit Mandelbrot has had a remarkable career which includes seminal work in theoretical and applied mathematics. Mandelbrot might be largely unknown to the wider world, but for the beautiful pictures that can be produced on a computer using the fractal equations he popularized (including the famous Mandelbrot set, named after it's discoverer).
Most people who work in mathematics (or computer science, for that matter) write for an audience of their colleagues. The majority of Mandelbrot's writing falls into this category. As the horizon of Mandelbrot's mortality approaches, he seems to be working to establish his intellectual legacy. He recently published Fractals and Chaos (Springer-Verlag, 2004), which is a collection of some of his papers from 1979 onward. Mandelbrot's papers can be difficult reading for anyone who is not a skilled mathematician. Mandelbrot has also written for a more general audience. His book The Fractal Geometry of Nature (Freeman, 1982) can be read by anyone who has a solid high school math background and patience with an academic writing style. In publishing The (Mis)behavior of Markets Mandelbrot is writing for the general reader, who usually has no tolerance for mathematical equations.
The roots of the book The (Mis)behavior of Markets go back to 1961 when Mandelbrot was a new researcher at IBM. Among other things, he was working on using computers to analyze the distribution of income in a society. Mandelbrot's work echoed the work of Vilfredo Pareto and showed that many economic factors, including wealth, are distributed according to an inverse power law. While at Harvard to give a talk on his work, Mandelbrot saw a diagram on a chalk board that mirrored the distributions he was seeing for income. But in this case the diagram involved cotton prices. With access to IBM's computers (and programmers) Mandelbrot started studying cotton prices.
Around the time Mandelbrot was doing his work on cotton prices the work of Louis Bachelier was being rediscovered and embraced by the academic economics community. Bachelier claimed that the change in market prices followed a Gaussian distribution. This distribution describes many natural features, like height, weight and intelligence among people. The Gaussian distribution is one of the foundations of modern statistics. If economic features followed a Gaussian distribution, a range of mathematical techniques could be applied in economics. With Bachelier's work and some modern reinforcement, a new era in economics was born.
Unfortunately, as Mandelbrot points out in The (Mis)behavior of Markets, the foundation of this new era of economics was rotten. As anyone who has repeatedly put money at risk in a market over a long period of time knows, market behavior does not reflect the well behaved Gaussian models proposed by economists in the 1970s and 1980s. There are far more market bubbles and market crashes than these models suggest.
The change in market prices does not follow a Gaussian distribution in a reliable fashion. Like income distribution, market statistics frequently follow a power law. When a graph is made of market returns (e.g., profit and loss), the curve will not fall toward zero as sharply as a Gaussian curve. The distribution of market returns has "fat tails". The "fat tails" of the return curve reflect risk, where large losses and profits can be realized.
The behavior of markets reflects a complex system and fractal mathematics. Mandelbrot has been publishing papers on this topic for several decades. His earlier book, Fractals and Scaling in Finance (Springer-Verlag 1997) collects a number of these papers. The (Mis)behavior of Markets provides a readable summary of Mandelbrot's work in finance. This includes work on long range dependence and the Hurst exponent, fractal scaling in market statistics and the distribution of risk.
In The (Mis)behavior of Markets Mandelbrot argues that the Gaussian models for financial risk used by economists like William Sharpe and Harry Markowitz should be discarded, since these models do not reflect reality. Mandelbrot argues that fractal techniques may provide a more powerful way to analyze risk.
Unfortunately Mandelbrot does not explain clearly how multifractal techniques might be applied to financial data to provide a better estimate for risk and volatility. Perhaps at the behest of his co-author, Richard Hudson, there are no equations in the main body of the book and only a few in the notes at the end. This leaves the reader with only Mandelbrot's articles for reference and these do not make easy reading. At least one book, Iceberg Risk by Kent Osband has managed to mix a very readable narrative with sections of mathematics. For those readers who would like to explore Mandelbrot's ideas in more depth, it is to bad that Mandelbrot and Hudson did not do something similar.
Benoit Mandelbrot is a great mathematician, but he is not a practitioner in finance. In some cases the behavior of markets is not as clear as Mandelbrot seems to suggest. Mandelbrot's criticism that stock market returns (profit and loss) do not follow a Gaussian distribution is certainly well founded and is becoming increasingly accepted. But what Mandelbrot does not discuss is that the statistical behavior of markets seems to change depending on the time period examined for returns. In many cases 1-day returns in the stock market (buy a stock at 12:00 PM and sell it at 12:00 PM the next day) have a distribution that is close to Gaussian. As the return period moves out (e.g., 4-day, 8-day, 30-day...), long range dependence starts to appear and the distribution strays from a Gaussian distribution.
Mandelbrot does mention that markets seem to display regimes. But he does not delve in detail into how this might be reflected in market statistics. Mandelbrot mentions that there are periods where the market acts like a calm sea. In this case we might expect that the distributions will also be relatively well behaved and do not stray that far from a Gaussian curve. In other cases Mandelbrot describes the storms that beset markets. In these regimes, when the market is in the throws of a bubble or after a crash, we might expect that the distribution of return will have "fat tails", reflecting extreme behavior.
The (Mis)behavior of Markets is a readable book and may be satisfying for the intellectual tourist who wants to visit fractals and market behavior. For someone who wants to understand Mandelbrot's arguments in detail, or perhaps write computer software that models some of the behavior Mandelbrot describes, the book is unsatisfying, leaving only recourse to Mandelbrot's less readable papers or books on chaotic mathematics, which do not discuss market applications.
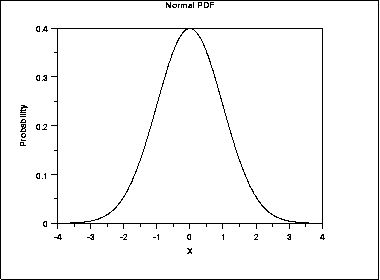
A Gaussian "normal" distribution is shown below.

One example of a power law curve with "fat tails" is the Cauchy distribution which is shown below. In the case of the normal curve, the tails are close to zero at -3.5 and 3.5. In the case of the Cauchy distribution the curve is still not close to zero at -5 and 5.
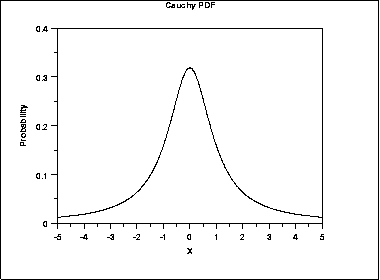
These plots are from the Engineering Statistics Handbook, 1.3.6.6 Gallery of Distributions published by the US National Institute of Standards and Technology.
A historical calculation of risk shows that it is not a "normal" Gaussian distribution. Rather, the distribution has "fat tails" (like the Cauchy distribution), reflecting more profit and loss than would be suggested by a "normal" distribution.
The future distribution of risk in markets is unknown and may be unknowable. The historical distribution of risk cannot be used to reliably estimate future risk, since markets are complex dynamic systems. Risk and its distribution is a constantly changing value.
Nassim Taleb's book review of (Mis)behavior of Markets (PDF format)
This is Nassim Taleb's beautifully written review of (Mis)behavior of Markets. Nassim Taleb is also the author of the book Fooled by Randomness, one of the best books I've read. On the basis of this book and his well respected book on options pricing, I have a lot of admiration for Taleb.
A review of Edgar E. Peters' book Chaos and Order in the Capital Markets
I was tempted to subtitle the above web page Modern Finance Theory on One Web Page. This web page summarizes most of the authors and high points of modern finance theory. What surprised me is that Mandelbrot is credited with being one of the parents of the so called "Efficient Market Hypothesis" (EMH).
The Working-Cowles-Kendall empirical findings were greeted with horror and disbelief by economists. If prices are determined by the "forces of supply and demand", then price changes should move in particular direction towards market clearing and not randomly. Not everyone was displeased with these results, however. Many viewed them as proof that the "fundamentalist" theory was incorrect, i.e. that financial markets really were wild casinos and that finance was thus not a legitimate object of economic concern. Yet others crowed that it proved the failure of traditional "statistical" methods to illuminate much of anything. High-powered time series methods were used by Clive Granger and Oskar Morgenstern (1963) and Eugene F. Fama (1965, 1970), but they came up with the same randomness result.
The great breakthrough was due to Paul A. Samuelson (1965) and Benoit Mandelbrot (1966). Far from proving that financial markets did not work according to the laws of economics, Samuelson interpreted the Working-Cowles-Kendall findings as saying that they worked all too well! The basic notion was simple: if price changes were not random (and thus forecastable), then any profit-hungry arbitrageur can easily make appropriate purchases and sales of assets to exploit this. Samuelson and Mandelbrot thus posited the celebrated "Efficient Market Hypothesis" (EMH): namely, if markets are working properly, then all public (and, in some versions, private) information regarding an asset will be channelled immediately into its price. (note that the term "efficient", as it is used here, merely means that agents are making full use of the information available to them; it says nothing about other types of "economic efficiency", e.g. efficiency in the allocation of resources in production, etc.). If price changes seem random and thus unforecastable it is because investors are doing their jobs: all arbitrage opportunities have already been exploited to the extent to which they can be.
I have interpreted the EMH as arguing that the markets follow a more or less Gaussian distribution, without long term memory. This is sometimes called "Gaussian-efficiency". This is not what Mandelbrot has argued exists in markets, so I'm surprised to see his name associated with the EMH. In The (Mis)behavior of Markets Mandelbrot seems rather caustic in his assessment of the EMH.
Mandelbrot and the Stable Paretian Hypothesis by Eugene F. Fama, The Journal of Business, Volume 36, Issue 4 (October 1963), 420-429 (from www.e-m-h.org)
What Mandelbrot referred to in one of his papers as a "stable Paretian" distribution is a power law distribution with "fat tails" (like the Cauchy distribution shown above).
Eugene Fama is widely viewed as the high priest of the Efficient Market Hypothesis, which I've always taken to infer Gaussian (or noral) distributions of return and risk. In a 1963 paper that echos some of the points make in The (Mis)behavior of Markets, Fama writes:
The fact that there are a large number of abrupt changes in a stable Paretian market means, of course, that such a market is inherently more risky for the speculator or investor than a Gaussian market. The variability of a given expected yield is higher in a stable Paretian market than it would be in a Gaussian market, and the probability of large losses is greater.
Moreover, in a stable Paretian market speculators cannot usually protect themselves from large losses by means of such devices as "stop-loss" orders. In a Gaussian market if the price change across a long period of time is very large, chances are the total change will be the result of a large number of very small changes. In a market that is stable Paretian with α < 2, however, a large price change across a long interval will more than likely be the result of a few very large changes that took place during smaller subintervals. This means that if the price level is going to fall very much, the total decline will probably be accomlished very rapidly, so that it may be impossible to carry out many "stop-loss" orders at intermediate prices.
I assume that Fama later came to believe that evidence argued against a Paretian distrution.
The books here are listed in roughly increasing order of mathematical difficulty.
Chaos and Fractals: New Frontiers of Science by Peitgen, Jurgens and Saupe.
This book covers many of the concepts of fractals and chaotic mathematics, but largely uses high school mathematics. Highly recommended.
The Fractal Geometry of Nature by Benoit B. Mandelbrot.
This book is briefly discussed in the review above.
Chaos Theory Tamed by Garnett P. Williams.
This is a very readable and clear explanation of many of the ideas and the basic mathematics behind chaotic mathematics. The mathematics is high school level to first year college (an understanding of basic discrete mathematics, like summations, is needed).
Chaos and Time-Series Analysis by Julien Clinton Sprott
The mathematics in this book is at a higher level, but is still clearer and easier to understand than Mandelbrot's papers.
Nonlinear Time Series Analysis by Holger Kanz and Thomas Schreiber
This book covers many of the topics related to chaotic mathematics applied to time series, but glosses over some of the details. The mathematics is also more advanced, including some partial differential equations.
Ian Kaplan
October 2004
Last updated on: